 Author
Author |
Topic: Christian Freeling on inventing games (part 2) (Read 244570 times) |
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #15 on: Aug 14th, 2013, 6:49am » |
 Quote Quote  Modify Modify
|
It so happened that I didn't die but my father did, three months ago, not unexpectedly because he was ninety-three and suffered from Parkinson's disease. His death left me as an only child in the most-likely-to-die-next chair, but comfortably so, given a substantial inheritance and the fact that I'm not particularly bend on beating him at longevity.
Generally
I followed the abstracts forum and found it at least as interesting as usual, and I played some Havannah at LG and Inertia at Mindsports, but that was about all I could manage gamewise. Many forum discussions were about what makes the best abstract. There's the romantic notion of 'grail games', but what these should be seems arbitrary and subjective. Zickzack introduced a distinction between a 'game' and a 'ruleset' but has not elaborated, which is a pity because under deeper scrutiny I fail to see any objective criterion to support it. I do however have an intuitive notion of what he's getting at: sometimes good ideas have resulted in mangled games because of an inventor's preoccupation with certain 'rules regarding rules', in particular the dogmas of the Church of Cyclophobia and Hard Finitude. Admittedly I've taken note of these too, but not to the point of rejecting games for not complying, or marring games to have them comply. If my goals changed over the years it is because of a shift of interest. I've naturally drifted away from inventing games that can be assembled easily towards an arbitrary result, albeit in the full recognition of the fact that any such a game could actually turn out great. I don't want to keep anyone from trying. Instead I've focused on simple homogeneous games in the last couple of years, with a self-explanatory structure. The former seeks an intricate combination of object and mechanics, while the latter implies reducing inventor involvement and arbitrariness as much as possible. It may not necessarily render the best game as Nick Bentley pointed out, but such a combination nevertheless tends to be trustworthy, with an 'organic' quality that usually begs and rewards investigation. I prefer to start by choosing an object because the question "what does it want" naturally precedes "how does it do it".
Specifically
You have been able to follow the process of invention of Inertia from a flawed Ayu clone to something completely different. So I'd like to shine a light on what that is.
What is not original about Inertia?
* The material is emphatically traditional.
* The rook move is the primary slider on a hex board.
* The object - unification - is identical in idea and execution with the object of LOA.
What is original about Inertia?
* The generic placement protocol.
* The generic restriction rule regarding movement.
Further characteristics are that the game couldn't be simpler, well … I couldn't make it simpler but if anyone can my mind is open. Draws by simultaneous unification are possible, and forced cycles may be possible. Base-5 would seem to be quite large enough to reveal its full scope, and a square version will most likely be base-8 and certainly connectivity-8, because the game doesn't need much material to reveal its depth and connectivity-8 sharply reduces the density at the end of the placement stage, if compared to connectivity-4.
The placement protocol
Coined "one sticking, one free", this opening protocol is a generic way to start games that benefit from an evenly divided initial position with a variably density. Inertia is one such game.
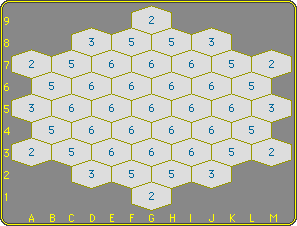
During this stage there's always one stone sticking for every free stone, so everything comes in pairs. The reverse is not true: that terminates the protocol. The last sticking stone may be of either color, so either color may end up moving first in the second stage. If we assume on theoretical grounds that it is good to have that first move, then the placement stage can be considered as a game in itself, and a far from trivial one at that. On a base-5 board the placement stage may end with as few as 2x7 stones, Red to move, or as many as 2x18 stones, Black to move. These are likely the extremes that are possible. Here's an example of the first:

And here is an example of the second, last placements are indicated in both examples.

Both have been achieved by legally knitting around and inward. It means that density after the opening stage in Inertia can vary between 23% and 59% and that's what makes getting the first move in the second stage against matching opposition so difficult.
Actual play
I played a lot of games against Jos Dekker at mindsports and a couple of games against different opponents at the 3rd Hexx6 Tournament, 13 July 2013 in Hilversum. Here's a photo of Pascal Huybers (white) against Ton van der Valk:

What struck me most, initially, was that it felt a bit like Othello and LOA when I first played those: a desperate search for some permanency and solidity. Othello and LOA are excellent games, but not wholly my taste, though obviously some players' taste, or they would have vanished. As an inventor I'd go for an excellent game that isn't wholly my taste anytime, so I kept playing despite the fact that Jos won most of the time. Jos likes the game and may have more of an intuitive feel for it, though that may change with experience. We also turned to playing base-5 most of the time, because the game gains clarity with decreasing material. Here's an example of a game I resigned after Red's 20. F56. Why? Because I was too lazy to look closer.

Red threatens to win with CG7 and 20…D47 is the only defense. Red cannot capture this stone nor can he capture F6G7x, both because of 21…F26. Moving 21.C74 loses on F25! (not 21…DF7? 22.CF4! and Red wins). The really nasty reply is 21.H8G7x:

Now capturing G67x or DG7x loses on 22.FC6 while GF6x loses on 22.GD7x. I thought for a moment that I could force a draw by simultaneous unification by 21…F26x, but instead of 22.GD7x? Red plays GE7!!

Now Black cannot split his double (unless by 22…FD6 or FC6 which both lose) and neither can he move the isolated stone. So he must move one of the double without disconnecting it from the other. Now Red moves 23.C76! and Black cannot prevent a red unification (that leaves Black with two groups) on the next move.
So … was I right to resign the game? No, I failed to consider the move, but after 20…D47 21.H8G7x I should have moved 21…F25 which secures at least a draw.

The threat is of course 22…DG7x. Capturing the lone black stone is an immediate Black win. F5 cannot be captured legally and 22.G76x loses on F56x while 22.FG6x loses on for instance F57 and 22.F67 loses on GD6!. So at least mistakes would have been competing for attention. The redeeming move for Red is 22.GF7 after which Black can force a draw with 22…GF6x. Now capturing the lone black is a draw and not capturing it but moving 23.FE7 (to prepare 24.C76 and try to unite without capturing) meets with 23…FE5!.

Black threatens to connect at D5 or F7 (if E7 is vacated) so Red is forced to simultaneous unification. As said, I should have looked more closely. 
|
| « Last Edit: Aug 14th, 2013, 6:50am by christianF » |
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #16 on: Aug 18th, 2013, 5:01am » |
 Quote Quote  Modify Modify
|
I've already posted the density range at the end of the placement stage on a base-5 hexboard: 2x7 to 2x18 stones, or 23% to 59%.
Pretend for a moment that the placement stage is the whole game and the player who moves last loses. So these are the rules:
Quote:Red starts by placing one stone on the empty board. From that point on players take turns to:
* Place a stone on a cell adjacent to the last stone placed by the opponent, and ...
* ... place a stone on a on a cell that has only vacant cells as neighbors.
Both placements are compulsory. When the player to move can no longer make the second placement, then his opponent wins. |
|
Now try it on a chess board, using connectivity-8 (so a diagonal stone is a neighbor) and you'll discover that the density range at the end of the game may vary between 2x6 stones and 2x19 stones, or 19% to 59%.
If you play it you may find it a surprisingly more difficult game than the simplicity of the rules would suggest and I never would have expected the highest possible density to be be more than three times as high as the lowest.
Did anyone?
edit
Haha, probably not. My abilities as a puzzler have always been questionable 
The 2x6 isn't that hard:

But I've not come beyond 2x16 in the highest density attempt, probably missed an illegal move in the previous one. I'll have a closer look at it.
edit
I did and it's 2x16 max if I'm not mistaken again. Minor mess up. 
Ed has implemented a base-8 connectivity-8 square version of the game. If you're not registered at mindsports, choose 'Inertia' in your prefs. If you challenge someone, the option "sq-8" will appear (next to "hex-5/6/7").
But ... a chess board and draughtsmen will also suffice. It's always nice to invent a new and hopefully interesting game for standard material.
|
| « Last Edit: Aug 19th, 2013, 3:55am by christianF » |
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #17 on: Aug 22nd, 2013, 7:55am » |
 Quote Quote  Modify Modify
|
Take a natural number 'N' and split it into natural numbers so that n1+n2+n3+ ... +nk=N.
Now consider n1 ... nk to be factors such that n1*n2*n3* ... *nk=K.
What is the maximum value K can reach?
Obviously no 'n' should exceed 4 because '5' can be split in 2 and 3 and these factor to 6, increasing K with one fifth of its value.
Now take the Symple move protocol, where you have the choice to add a new group or grow all existing ones, and let the groups represent 'n1 ... nk'. In order to maximize 'K' you'll have to create multiple groups, but none of them, ideally, should exceed 4 stones. Under compulsory placement this creates a beautiful and ice-cold dilemma: you need many groups yet must avoid having to connect them. Connections kill!
Evenf one would not have the total score available, strategy, both overall and local, would be fairly clear, without the need for a calculator. But of course the applet will constantly keep track of a) the number of stones, b) the number of groups and c) the score.
Needless to say that the protocol's embedded turn-order balancing mechanism adapts itself seamlessly.
The game may end in a draw, even on a hexhex- or an odd-sized square board: imagine both players having groups that are equal in size and number, but one player has an isolated extra stone. I don't care to much about draws (who started that decisiveness nonsense anyway?), but here's an elegant way to avoid them altogether: in case the same endscore 'F', the player with the least number of stones wins on efficiency grounds.
If this is not a quintessential 'product' game, then there must be one that is simpler and equally self-explanatory.
It's called Multiplicity. As in Symple and Inertia the inventing process was hexagonal and implementation will be square. It may take a while though because we've got quite a pipeline and the going is slow. The season is approaching, but I hope I can avoid new games this year and catch up on last year's stuff.
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Inertia
« Reply #18 on: Aug 23rd, 2013, 5:36am » |
 Quote Quote  Modify Modify
|
So get out yer chess boards and draughtsmen and give it a try. I't not all that long a game either: I lost this one fairly quickly, which is annoying considering the number of hexgames I played. I take comfort in the thought, whether true or not, that good players are usually bad inventors and vice versa. 
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Relatively absolute ...
« Reply #20 on: Sep 1st, 2013, 6:41am » |
 Quote Quote  Modify Modify
|
Take a 7-cell hexhex section and put 3 black stones alternating on the edge. Now add a black stone in the center: how can it be captured? Obviously, in doing so, you turn 1 black group into 3, so you have to simultaneously merge 3 red groups into 1. This is possible if and only if 2 remaining edge cells are red (and separated) and a single captures along the entrance line of the last free edge cell.
There's a square equivalent where black occupies 3 corners and the center of a 9-cell square section. To capture the centerstone Red needs 2 stones on opposite sides of the centerstone and a single that can enter along one of the remaining orthogonals or the one remaining diagonal.
But if Black were occupying all four corners, then the centerstone would be absolutely safe from capture, a situation that cannot occur in the hexversion of the game.
Of course even that is 'for the time being', but it's nice to discover something absolute in Inertia, even if it's relative. 
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
It isn't always a close finish either ...
« Reply #21 on: Sep 1st, 2013, 8:59am » |
 Quote Quote  Modify Modify
|

|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #22 on: Sep 2nd, 2013, 5:30am » |
 Quote Quote  Modify Modify
|
In Multiplicity groups are factors. Now consider the square grid, say a chess board, and connectivity-4. Putting a black stone on every black square and a white one on every white square, and you have 2x32 groups (and an equal endscore of '1'). What's the point?
Well, you can't have that many seperate groups on a hexboard. The question 'what is the maximum number of black and white groups in any distribution on a base-N hexhexboard' may be interesting in this context (2N-1 presents itself). In any case, it is far less than c-4 groups on a square board.
So on a hexgrid groups, whatever their number, will eventually be forced to merge into bigger groups, or in other words, scores will be forced down earlier than on a square board. The more groups, the faster they will be forced to merge.
Multiplicity will behave in a similar way on both grids, but not to the same effect. Scores on a square grid are likely to be higher, and the trimming down of the scores by forced connections towards the endgame, will start later and probably be less dramatic. In terms of gameplay the hexgrid would appear to offer more drama and at an earlier stage.
These considerations are in part build on a solid insight in the nature of the Symple move protocol and the way it interacts with this particular object. That interaction would seem even more intricate than in Symple itself. After all, Symple needs an artificial entity to make it work: the group penalty. Multiplicity's goal is less than usual, but wholly natural.
|
| « Last Edit: Sep 2nd, 2013, 6:33am by christianF » |
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #23 on: Sep 17th, 2013, 11:32am » |
 Quote Quote  Modify Modify
|
Chaosu at LG pointed out that the "one-sticking-one-free" opening protocol might serve Lines of Action itself, though to what effect?
The "one-sticking-one-free" protocol is a game in itself, that results in a variety of opening opsitions for a variety of omni-directional games, such as LOA for instance. On a 8x8 board with connectivity-8, the average density of the resulting positions has been 11.7 men per player, ranging from 2x10 ...

... to 2x14. Last placement indicated in both cases

That's higher than LOA, but maybe not annoyingly so.
The effect, in my view, would be similar to the effect of the Chess-960 opening protocol for Chess: increased scope for and dominance of tactics, and a strategy that must be formulated in more general terms. The opening theory based on the specific opening array of LOA would not be applicable.
It may be fun, or maybe not, but in any case it shows the wide field of games to which the "one-sticking-one-free" protocol may be applicable.
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #24 on: Sep 21st, 2013, 9:09am » |
 Quote Quote  Modify Modify
|
It's that time of year again so I feared it might happen, and it did. I found a new game. Just an hour ago a crucial missing part fell into place.
Material
Cemetery is played on a chess board. There are two players, black and white. Each has a sufficient number of draughtsmen at his disposal. In addition there's a sufficient number of tombstones.
Definitions
* The "capacity" of a square equals the number of orthogonally adjacent squares.
* Pieces are "stacks". A single man is a stack of one. Stacks may have any composition and are controlled by the player on top.
* A "zombie" is a man that has been returned to its owner in the course of the game, to be used at a later stage.
* A "tombstone" removes a square and thus reduces the capacity of the adjacent squares by one.
Rules
The game starts on an empty board. There are two stages, the placement- and the movement stage.
The placement stage
This stage follows the 'one-sticking-one-free' opening protocol. White starts by placing one man on the empty board. From that point on players take turns to:
* Place a man on a square orthogonally adjacent to the last man placed by the opponent, and ...
* ... place a man on a square that has only vacant orthogonal neighbors.
Both placements are compulsory. When the player to move can no longer make the second placement, then his turn ends and his opponent may start the movement stage. The number of white and black men will always be equal, although the 'density' of the position may vary and either player may end up being the one to start the next phase, depending on whether the number of full turns was even or odd.
The movement stage
On his turn a player either moves one of his stacks or enters a zombie.
* A stack moves horizontally or vertically, based on the number of pieces to be moved (e.g. one piece moves 1 square and a three-piece stack moves 3 squares). Stacks may be split in this process: a player may choose for instance to move only the top man or the top two men of a higher stack. Stacks may move over or onto any square, whether vacant or occupied, but they may not move over or onto a tombstone.
* Instead of moving a stack, a player may choose to enter a zombie on any square, whether vacant or occupied.
Capture, with or without resurrection
* If moving or entering causes a bi-colored stack to surpass the capacity of its square, then the moving player's men in it return to his stock of zombies, while the opponent's men are removed from the game. At the same time a tombstone is put on the square.
* Erecting a tombstone may cause a bi-colored stack on an adjacent square to surpass capacity. Such a stack is removed in the same turn causing another tombstone to be erected. Chain reactions are possible. Regardles of whose color is on top in follow-up captures, the moving player's men add to his stock of zombies, while the opponent's men are permanently removed.
Object
A player wins by eliminating the opponent, that is leaving him without stacks and zombies.
Cemetery © Mindsports
Edit 1:
It is logical to apply the concept of "capacity" only to bi-colored stacks. High mono-colored stacks then pose a severe liability, rather than being a means to erect tombstones while retrieving zombies, as they would otherwise. It also eliminates the possibility of players co-operating to completely blanket the cementery with tombstones, while still having zombies.
Edit 2:
"Reserves" have become "zombies", courtesy of meadmaker 
Edit 3
As for having a provisional shot at Cemetery's behaviour, obviously the basis is a mechanism similar to Focus' way of accumulating small material advantages, like the extra captured man or the extra retrieved zombie. Such advantages grow with diminishing material. In that sense the basis provides little room for drama.
Linking capacity to the number of neighboring cells isn't new. I did that in Crossfire, providing the mechanism with a new kind of tactics: aiming large stacks at low-capacity cells. What is new is to make 'capacity' variable in the process, by introducing tombstones. Since every tombstone causes at least one man to be permanently removed from the game, their maximum number will be less than the number of men on the board. Their tactical impact will be clear:
* They constitute obstacles, lowering mobility but introducing some positional aspects.
* They lower the capacity of adjacent cells, allowing for quicker but less dramatic captures.
The emergence of tombstones may cause formerly critical stacks to surpass capacity. If such a 'secondary' stack belongs to the opponent, the moving player yet wins it as if he had been in top. That's a taste of drama. Chain reactions will occur occasionally, but there's no positive feedback, so they will usually be limited to say one or at most two follow-up captures.
|
| « Last Edit: Sep 23rd, 2013, 10:17am by christianF » |
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #25 on: Sep 29th, 2013, 8:55am » |
 Quote Quote  Modify Modify
|
Recently I found myself back in Tampertown. After all these years I thought it a good idea to visit the cemetery and pay tribute to all the dead inventors. On my return I did some tampering myself (in red), because I had just the right game for it. 
Tampertown Cemetery
Every year on Walpurgis Night the dead at Tampertown Cemetery rise from their graves to engage in their annual "Kill the Undead Dead" celebration.
The cemetery counts 48 graves around a small chapel in the center.
All graves are open for the night, and every grave has two, three or four graves called 'neighbors' immediately next to it.
The number of such neighbors is important. There are initially 12 graves with two neighbors, 16 with three, and 20 with four.
There are two zombiemasters, Red and White. Each has a sufficient number of zombies at his disposal. In addition there's a sufficient number of tombstones.
Definitions
* The "capacity" of a grave equals the number of its neighbors.
* Zombies operate in stacked "groups". A single zombie is a group of one. Groups may have any composition and are controlled by the color on top.
* A "tombstone" removes a square and thus reduces the capacity of its neighbors by one.
Rules
The game starts with the dead eagerly waiting to rise from their open graves. There are two stages, the resurrection- and the movement stage.
The resurrection stage
Zombies rise in pairs from adjacent graves, side by side, one of each color. The White master starts by resurrecting one corpse from a grave he chooses. From that point on masters take turns to:
* Resurrect a corpse from a grave next to the corpse just resurrected by the opponent, and ...
* ... resurrect a corpse from a grave that has only open neighbors.
Both resurrections are compulsory. When the master to move can no longer perform the second resurrection, then his turn ends and his opponent may start the movement stage.
The number of white and red zombies will always be equal, although the 'density' of the teams may vary and either master may end up being the one to start the next phase, depending on whether the number of full turns was even or odd.

Here's a position at the end of the resurrection stage. Red's last move was the placement at C2, White now starts the movement stage.
The movement stage
On his turn a master either moves one of his groups or enters a zombie.
* A group moves horizontally or vertically, based on the number of zombies to be moved (e.g. one zombie moves 1 grave and a group of three moves 3 graves).
Groups may be split in the process: a player may choose for instance to move only the top zombie or the top two zombies of a larger group.
Groups may move over or onto any grave, whether open or occupied, but they may not move over or onto a tombstone.
* Instead of moving a group, a master may choose to enter a zombie on any grave, whether open or occupied.
Capture
* If moving or entering causes a bi-colored group to surpass the capacity of its grave, then the moving master's zombies in it return to his stock of zombies, while the opponent's zombies are removed from the game.
At the same time a tombstone is put on the square. There is one exception to this: a mono-colored group may not be captured by entering.

White has just moved H5-H3. Despite the fact that H3 is now 'on capacity', Red cannot capture this group by entering.
However, entering on H3 does result a bi-colored group that either player can capture by entering there on his next turn.
* Erecting a tombstone may cause a bi-colored group on an adjacent grave to surpass capacity. Such a group is removed in the same turn causing another tombstone to be erected. Chain reactions are possible.
Regardles of whose color is on top in such follow-up captures, the moving master's zombies add to his stock, while the opponent's zombies are permanently removed.
Object
A player wins by leaving the opponent without any group on the board, regardless of how many zombies remain in either stock, or whether his own last group disappears from the board in the process.
Tampertown Cemetary © Mindsports
By the way, both the applet and the game are still in Tampertown, but here's our first game. I feel I'm in somewhat uncharted territory here regarding endgames and the role of forced cycles, so let's look if and when "the ship runs ashore", to use a literal translation of a dutch expression.
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #26 on: Oct 2nd, 2013, 3:21am » |
 Quote Quote  Modify Modify
|
I'd like to direct some attention to Tampertown Cemetery. Our first game was somewhat flawed in that the code had to be adjusted regarding the legality of entering on a opposing mono-colored group, yet it allowed a glimpse of some interesting tactics. More about that later.
Remember Nick's post at BGG? Here's a quote:
Quote:In contrast, I think great games are unclear; they make it hard, really hard, to identify good moves, but they do something else to make up for it: they excite in the mind ideas for moves which seem good, but actually aren’t. This has two important effects:
1. it gives players the needed sense of direction and competence even when they’re playing a deep game and in fact have no idea what they’re doing.
2. it sets players up to be surprised when they discover their initial ideas were wrong – in other words it creates Eureka moments, which are among the supreme joys of playing a good abstract game. This is only possible if a game stimulates compelling but ultimately incorrect ideas about how to play well.
I call this quality "Speciousness" (I used to call it False Clarity until I realized there was a perfect word to describe the quality – Specious means "apparently good or right though lacking real merit; superficially pleasing or plausible").
The greatest games pull this trick over and over – just when you think you’ve learned everything, the scales fall from your eyes yet again, and yet again you realize the game isn’t quite what you thought it was.
source |
|
There's still David Buckley's question whether this constitutes any significant difference from Mark Thompson's concept of Clarity versus Depth, and I suppose it depends on what is meant by "clarity" and how it can differ for different players of the same game, depending on their level of play. But we had a perfect example of a Eureka moment in Tampertown. Before I come to that, let's first have a look at TC's structure, and compare it to the stucture of its ancestor Focus. This comparison is inevitable, so I'd better do it right to serve those who feel appearances may be misleading.
The motor: recycling reserves
Barring draws by exhaustion, what eventually drives Focus over the cliff are its recyled reserves. The influence of small material advantages tends to increase with diminishing material, and barring a very fine balance, the thing eventually goes one way or the other. That's the game's undercurrent and tactics go easier with the flow than against it.
Introducing the number of adjacent cells as a criterion for a cells 'capacity' works fine in Crossfire in that it provides some strategical solidity in a very 'fluid' environment: you can aim large center-columns at low-capacity cells along the edges and harvest the fruits. The criterion isn't anymore logical than Sid's choice of "5" in Focus, but it seems less arbitrary.
A chance encounter of ideas
Chance encounters of ideas are always a part of the process. I had trashed "Trounce" because it had an annoying smell of something being wrong despite my failure to find it. It set my mind on the quest for something simpler. That means juggling with ideas, mechanisms and principles during the daily routine.
The exact time of birth of TC was when I realized that the principle of recycling reserves in Focus could be implemented with a different mechanism. Instead of stuffing men from above and harvesting the surplus from below, one could remove a whole bi-colored column once it had surpassed its 'capacity'. Capacity would be determined by the number of a square's neighbors. If the square itself were to be removed after a capture, the capacity of each of its neighbors would be reduced by 1. Sub-critical columns on such squares would suddenly be critical, while critical columns would raise above their limit and thus be captured in the same move. Chain reactions would be possible. The board would consist of ever less squares with a decreasing average capacity. Since every capture requires at least one man to be removed permanently, the number of blocked squares would never surpass the number of men. Since 'entering' is part of the mechanism, isolated areas would present no special problems. That was the moment of its birth. It took considerably less time to see it than to write it down.
Tampering
The board I eventually chose serves the mechanism: it has 12 capacity-2 squares along the edge, 16 capacity-3 squares, half of them along the edge and half around the chapel (apart from pittoresque and thematic aspects the chapel only serves to add 8 capacity-3 squares to the center) and 20 capacity-4 squares.
It was already impossible to get reserves without capture (that is: you cannot capture mono-colored groups of your own), so capture was restricted to bi-colored groups or groups belonging entirely to the opponent. Since I prefer generic rules, there was initially no difference between 'capture by moving' and 'capture by entering'. However, unrestricted capture by entering seemed to lead to lack of solidity and a tensed up game because entering on a sub-critical group would always 'expose' it. Forbidding it altogether could lead to capping and recapping the same group till one side was exhausted. So I came to a logical balance: you cannot capture a mono-colored group by entering. Since there are ample capacity-2 squares, this allows a player to enter a single there, and another one and another, and all the while the opponent, who makes the column bi-colored if he enters there, runs the risk of having it captured next move. A mono-colored group can thus relatively safely grow, and move as long as it doesn't sink below sub-capacity. It provided the solidity I was after.
I also decided to make presence on the board, or indeed lack thereof, the deciding criterion for winning or losing. This advances the critical point in endgame situations. It led to unexpected endgame tactics.
A Eureka moment
We initially considered entering on a (sub)critical mono-colored group as dumb: why enter there if you can be captured next move? Why not simply forbid it?
And that's what Ed did, provisionally, because the codechange required was minimal. But I had my doubts, both by experience and principle. I had doubts whether capping a (sub)critical mono-colored group would under all circumstances be dumb. I know the tricks games can present one with. I also find, on philosophical grounds, that rules are not there to prevent dumb moves.
Ed agreed but now faced a problem he had tried to avoid: the applet would simply consider every square at the end of a move, and execute a capture if a bi-colored square was above its limit. By allowing a bi-colored group above capacity to exist, he had to rewrite the code accordingly.
Meanwhile we were continuing our game and I want to draw your attention to (R)ed's 24...G3. It threathens to capture H3 and I can't escape to E3 (because of the groups at B3). I can cap it once, but not twice. Fortunately I found 25.HF3 and now Red cannot move G3 to either side, because both would turn critical. Or so I thought.
But Ed moved 25...FE3 just the same, and I wondered why. Of course I captured 26.F3. Then came 26...H3! It was the 'dumb' move, at that point only possible because it didn't surpass capacity, because Ed hadn't changed the code yet. But I had it there for the taking. Why wouldn't I...? And then the "Eureka" moment kicked in. Capturing H3 would lose the game because it would leave only one white group at B2, and this last group would simply be capped. Suddenly there was a less than dumb reason for playing the 'dumb' move, and not as a result of a tactical peculiarity either, but rather as a structural aspect of endgames: if you're down to two groups and the opponent caps one of them, you cannot capture it!
Endgame peculiarities
I've not yet puzzled out the extremes, but you get between say 10 to 15 pairs of zombies on the board. These are stacked in groups while some go permanently off the board, some temporarily. Pretty soon one or both players will be down to three groups. If then a sub-critical one is capped by the opponent and the player captures it, he will be down to two groups. That means he cannot capture anymore if one of them is capped, but must enter instead. This of course can already be the point of a combination: The capped piece is now under the opponent's control and may cause an immediate threat. These tactics result from leaving reserves in hand out of the equation in terms of the win condition.
Finally, notice that the endgame was decisive from an almost symmetrical position with only a few pieces left. TC implicitly has cooperative cycles, and I strongly suspect that there are positions possible that resolve in a forced cycle. But I don't think their appearance will be frequent. Draws by exhaustion are possible of course, and in exhausted endgames sides may end up without reserves and in isolated territories. But that, I expect, will not be a frequent occurence either.
We've engaged in a second game and a third one under its full name. The applet works fine now and the game has been fully implemented. I thank Ed for that, and I invite those of you who at least halfway trust my judgement to join us in the player section for some new and surprising tactics.
|
| « Last Edit: Oct 2nd, 2013, 10:42am by christianF » |
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #27 on: Oct 3rd, 2013, 4:58am » |
 Quote Quote  Modify Modify
|
This question came up recently at BGG;
Quote:It occurs to me that I may not fully understand what you mean by "organic". For example: maybe you would consider Slither's rules just as organic as Crossway's?
I think I've been taking it to mean: some combination of simple + intuitive. Is that right? |
|
Nick Bentley, actually. Apart from being simple, homogeneous and answering one basic principle, there's this (answer reposted from BGG):
Tampertown Cemetery made me realize a prime characteristic of organic games: they act on a 'plain plane'. The point shows in what I consider my major games of the last three years Symple, Sygo, Inertia and (yet veiled) Multiplicity. They all use plain boards and they're all scalable. Boardsizes should be practical, but they allow different shapes. All are possible on both square- and hexboards, though gameplay may favor one or the other. Edges and corners have no special role apart from their inherent necessity and its consequences in terms of strategy and tactics. An organic game is something you release on a plane.
In contrast, TC is a merger from different principles and mechanisms, pointing to a particular board-structure to optimize its behaviour. Putting it on a hexboard immediately gives problems. I only mention the fact that you need capacity-2 cells to (relatively) safely start a group. A Crossfire board would do:
But then, with the OSOF protocol you don't get enough zombies in the yard to climb to capacity-6 and over.
So TC isn't like releasing an organism on a plane, but more like starting up a mechanism in a prepared playground.
In terms of gameplay there's no value judgement implied, I just like the natural ones better. But I couldn't resist a Tampertown detour. 
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #28 on: Oct 4th, 2013, 7:51am » |
 Quote Quote  Modify Modify
|
Let me elaborate just a tiny bit on TC's strategy. Take a position a couple of moves beyond the opening phase, with two or three tombstones and each player having one or two reserves in hand. You're Red and you have two groups, A and B, both composed of a red zombie on top and a prisoner underneath. A and B are one square straight apart, so A can jump onto B and vice versa. However, both A and B occupy capacity-4 squares, so either jump only brings the resulting group 'on capacity' and ready for the taking by the White, by simply capping it with a reserve.
White cannot enter on either group because the other would then jump and capture, but to complicate matters let's say group A is also under attack by a White group of two (also on a capacity-4 square, lest it should be captured by A). So Red cannot enter a reserve on A in preparation for a jump by B, because A would be captured before B could jump.
But he can enter on B because B is not under attack by a white group of 2 so if Red enters on B, white cannot capture. Now Red has a group of 2 on A and one of 3 on B, and moving A onto B captures two prisoners and gives three reserves. White cannot prevent that by moving his two-group onto A, because that's still four on a capacity-4 square and it triggers a Red reply of moving two of the three zombies of B onto A catching a mixed total of six.
This little scenario that can be explained without so much as a board, comes in a number of variations the key theme of which is capturing the extra prisoner and/or getting the extra reserve to dominate events.
|
|
 IP Logged IP Logged |
|
|
|
christianF
Forum Moderator
Forum Guru
    

Arimaa player #4019
Gender: 
Posts: 804
|
 |
Re: Christian Freeling on inventing games (part 2)
« Reply #29 on: Oct 5th, 2013, 12:36pm » |
 Quote Quote  Modify Modify
|
This one, the last one under its first name, has ended in defeat for me. Note that White cannot capture by entering at A4 or C5 because Red then wins by capping C2. The group at C2 has been severely handicapped since its appearance on F2. If Red enters on it now, White can wave the world goodbye in a suicide capture!
Despite my loss  (that was a joke, actually) the game till now behaves as intended and expected. Better actually, I expected tactical surprises but not to this extent. (that was a joke, actually) the game till now behaves as intended and expected. Better actually, I expected tactical surprises but not to this extent.
There must be draws hidden in this pit, but we've not seen a shadow of them yet.
I know "fun" is the least useful word to put on a game, but I see no alternative. 
This one, the first one under its proper name, shows an updated applet with a "dead & buried zombies" counter and a move indicator. There's some casual comment included that does little justice to Ed's excellent strategy (from a rookie's point of view) of creating sub-critical groups that made it difficult for me to enter. Eventually I was immobilized while having more material!
|
| « Last Edit: Oct 6th, 2013, 12:40pm by christianF » |
 IP Logged IP Logged |
|
|
|
|